Wildcards can be described as a stripped-down version of Regular expressions, but they are often used to match file names (e.g. fnmatch, glob).
The two most common metacharacters are question mark ? and star *. Question mark represents a single character while star represents zero or more characters.
Question mark is analogous to '.' and star is analogous to '.*' in regex.
Many command line utilities also support wildcards. For instance, ls *.c means list every file with a .c extension.
Some time ago, we needed a fast and reliable wildcard matching algorithm for our AntiMalware product. More specifically, we needed it to match hundreds of thousands of paths across our suspicious path list. For a computer with 500,000 files and a suspicious path list consisting of 10,000 wildcard paths, this algorithm would need to handle five billion comparisons.
I will discuss different matching approaches here with code examples and compare their speeds. I will also apply some basic optimizations to them.
Recursive algorithms result shorter, cleaner and more elegant code, but they are usually slower than iterative counterparts. The most common wildcard implementations are recursive.
If we don't have a star in the pattern, algorithm is plain for both iterative and recursive form. We iterate through pattern and string simultaneously, if the characters match (remember that ? matches any character) and both strings end at the same time, it's a match.
If we have a star, it's a little more complicated. Once we encounter a star, it's a safe point to revert in case of a mismatch; as long as we have more string to process, we may still have a match. Therefore, we need to keep track of the star's location. This is the key to every algorithm.
There is a catch here. If we have multiple stars in the pattern, we need to keep track of only the latest one; we already had a partial match until that star, and there is no point in reverting previous stars unless you are trying to find all possible matches. This reverting process is called backtracking; we'll discuss it in greater detail and show a way to avoid it later in the NFA Algorithms section. For now, let's examine the recursive function below.
int EnhancedMaskTest(char *mask, char *name) { for (;;) { char m = *mask; char c = *name; if (m == 0) return (c == 0); if (m == '*') { if (EnhancedMaskTest(mask + 1, name)) return 1; if (c == 0) return 0; } else { if (m == '?') { if (c == 0) return 0; } else if (m != c) return 0; mask++; } name++; } }
I've found this function in 7Zip's source code. Wildcard pattern is the mask parameter and regular string is the name parameter. It returns 1 in case of match and 0 otherwise. I modified it slightly; you can find the original source code here.
If the function encounters a star, it calls itself (i.e. recurses) with the rest of the name and mask. Notice that it skips the star in the mask; otherwise the function would call itself forever.
If there is a match from the subsequent calls, we will return 1 and the function will end with a match. Otherwise, we will iterate through the name but not the mask. Note that mask is incremented only in the else block if the characters match. This recursion implicitly means saving the star's location. We are saving it by keeping mask the same, but incrementing name and trying to match again.
Let's see an example. Our pattern is test*mask and our string is testingmask. The first four characters will be matched without a problem; when we encounter the star, however, we will recurse with name=ingmask and mask=mask. Hereby, we have a brand new call with mask and ingmask parameters. It's an obvious mismatch, so the subsequent call will return 0.
Consequently, we will not alter mask, but we will increment name and recurse again. Here is the call flow with parameters.
Call mask name --------------------------------------------- 1 test*mask testingmask (Original call) 2 mask ingmask 3 mask ngmask 4 mask gmask 5 mask mask (Match)
The function will be called five times and the fifth call will return 1; therefore, the function will end with a match.
This function is inherently slow, but there are some pathological cases that make it run forever. For instance, if we call it with the parameters mask=*********a*********b and name=aaaaaaaaaaaa.zip, it ends in ~10 seconds. It takes exponentially more time as we give longer inputs.
There is a small optimization to resolve this problem, namely collapsing multiple stars. It reduces number of recursions substantially. See the modification below. This version ends in ~3.2 microseconds with the same parameters.
int n = 0;
while (m == '*')
m = *(mask + ++n);
if (EnhancedMaskTest(mask + n, name))
Iterative algorithms share most of the same semantics as the recursive ones except they are usually faster. There is a small difference however, in recursive functions; arguments are copied and subsequent calls have their own copy of arguments in the call stack, and the original function's state is not affected by the subsequent calls. Therefore, returning from the function is sufficient to revert the previous state.
In iterative algorithms however, we should explicitly save pattern and string locations to revert in case of a mismatch. Let's see the iterative function example below. This function is used in our Mobile Antivirus product.
int wild_match_iter(char *pat, char *str) { char *locp = NULL; char *locs = NULL; while (*str) { /* we encounter a star */ if (*pat == '*') { locp = ++pat; locs = str; if (*pat == '\0') { return 1; } continue; } /* we have a mismatch */ if (*str != *pat && *pat != '?') { if (!locp) { return 0; } str = ++locs; pat = locp; continue; } pat++, str++; } /* check if the pattern's ended */ while (*pat == '*') { pat++; } return (*pat == '\0'); }
As you will notice at first glance, pat is wildcard pattern and str is regular string. Local variables locp and locs keep revert locations for pattern and string respectively.
When we encounter a star, we'll save pat and str locations in order to revert these states later. Notice that we don't revert to the exact same state (we would have an infinite loop if we did); instead, we increment the saved strings location (++locs) and return to that state.
Therefore, as in the recursive algorithm, we keep the pat same, but increment str and try to match again.
Finally, when the str is finished, we check to see if the pat is also finished. Note that patterns may have trailing stars since star means zero or more characters. We skip those stars and check if the pat is finished, then return accordingly.
When we have a mismatch, we always keep the pattern the same, but increment the string one letter at a time and restart the matching process. That's expensive especially in recursive algorithms. There is a simple optimization we can apply to both algorithms.
Consider that we have a pattern *days and a string lovely_days. Our pattern starts with the letter d, so any string that doesn't start with a d doesn't have a chance to match our pattern. Hence, before trying to match again, we quickly look up for the next d in the string, which allow us to skip seven letters lovely_ that don't have a chance to match anyway.
Nondeterministic Finite Automata (NFA) algorithms are inherently different from the previous ones, because they don't involve backtracking.
NFA is used in Regex engines extensively and there is an algorithm, called Thompson's construction, to transform a regular expression into an equivalent NFA. It was developed by the greatest living computer scientist Ken Thompson—there is an inspiring article about it written by Russ Cox that you should definitely read.
The main point of these algorithms is that we carry forward all possible matches as we iterate the string, hence we don't need to backtrack in case of a mismatch. Since we iterate string only once and never backtrack, these algorithms have an advantage in situations involving heavy backtracking.
You don't need to know finite automaton in order to understand my code. I used the core idea without getting into details about states, transitions etc. for the sake of shortness. But you will see them used implicitly. If you are interested in the subject, I urge you to read Cox's article.
What does it mean to carry forward all possible matches? It means we have a list of patterns indicating all possible matches at the moment. As we iterate the string, we'll also iterate through every pattern in this list. New possible matches will be added to our list and some of them will be eliminated because of mismatches.
I'd like to give a glimpse into how do we add new possible matches to the list. In the beginning, we have only one pattern in our possibility list. It will stay like this until we see a star. When we encounter a star, we keep it saved and we'll use the letter followed by star for a special purpose. If our pattern is *nfa, this letter is n; everytime we come across with an n in the string, it can be the beginning of a possible match. Therefore, we should add a new nfa (anything we see after the star) to our possibility list before starting comparisons.
Eventually we will start comparing each pattern in our list with the input letter. Each pattern will be compared as though it was the only pattern just like in the previous algorithms. Some of them will match and will be incremented, while some of them will not match and will be eliminated. Notice that instead of backtracking, we only eliminate that pattern and continue with the rest.
Let's see an example.
We have a pattern x*dodo and a string xddodo. The first input letter is x and the only pattern in our list is x*dodo.
Both of them will be incremented, and we will have ddodo as the string and *dodo as the pattern. Things are getting interesting here; we have a star now, and therefore we know that whenever we come across a d, we will add a dodo to our possible matches list.
Let's see the steps: left column is input which is the letter we read from string at every step, and right column is possible match list (first line of it shows the list before the input processed, and second line shows after).
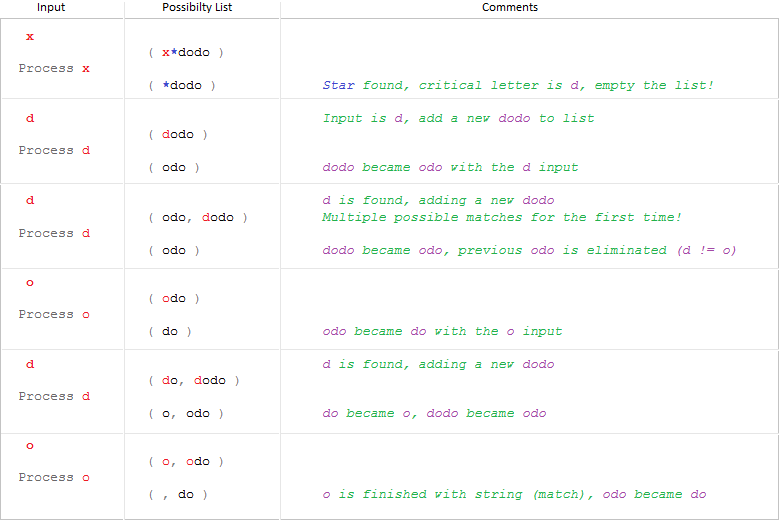
If we encounter a star, we empty the list; we don't need possible matches from the previous stars since we’ve reached a new star. Remember that if we had a mismatch in previous algorithms, we were reverting to the saved star location and saved string location + 1. This reverting process, called backtracking, is not necessary here because we carry forward all the possible revert points with us and compare them at every step.
To sum it up, we:
It's time to look at the code. It's naturally longer and more complicated than the previous ones. I had to set some limitations to make it shorter. The size of match list is 100, so we can't have more than 100 possible matches at the same time. In my real world test cases, it went to a maximum of five.
int wild_nfa(char *pat, char *str) { int i, nmatch = 0; char *star = NULL, *match[100]; match[nmatch++] = pat; while (*str) { if (star && (*star == *str || *star == '?')) { match[nmatch++] = star; } for (i = 0; i < nmatch; i++) { char *p = match[i]; if (*p == '*') { while (*p == '*') { p++; } star = p; if (*star == '\0') { return 1; } nmatch = 0; str--; break; } if (*p == *str || *p == '?') { match[i]++; } else { size_t ncopy = (nmatch - i - 1) * sizeof(*match); memcpy(match + i, match + i + 1, ncopy); i--, nmatch--; } } str++; } for (i = 0; i < nmatch; i++) { char *p = match[i]; while (*p == '*') { p++; } if (*p == '\0') { return 1; } } return 0; }
I'd like to make some clarifications and give implementation details to the readers who already know NFA algorithms. We don't have a structure for states—every letter in a pattern represents a state. Match list holds the list of states that NFA automata is at simultaneously. Transitions from one state to another are done simply by incrementing the pattern.
A major implementation difference is that when we encounter a star in any state, we empty the whole list. We are only interested in the latest star. Since we'll only have one star state at a time, we do not keep it in the list, but in a separate variable. Keeping star's state persistently mimics epsilon transitions in NFAs. These optimizations are good to keep the number of states minimal, and they bring no harm unless you want to find all possible matches. We are only curious about the match status.
To make it safer, we can add a line to check if nmatch is equal to 100, and exit in such case. We can also add an "if" statement to exit early if the match list and the star is empty at the same time, which means a mismatch. I skipped those to keep the code short.
I tested these algorithms along with two more algorithms I borrowed from others.
The first one is by Alessandro Cantatore (see his article) and the second is by Kirk J. Krauss (see his article). Both algorithms are iterative and backtracking. The third one is an optimized version of our iterative algorithm. Although Krauss's algorithm failed to pass my tests, I put it here because it claims to be fast and I used his test patterns. For instance, it fails to match the case, pattern=*aa? and string=aaaaa.
The test machine's specifications are the following. OS: Windows 7 64 bit, CPU: Intel i7-4770K @3.50 GHz, RAM: Kingston 16 GB DDR3 1600 MHz.
I compiled them with MinGW gcc version 5.3.0 with -O3 flag.
I have 87 test patterns and 95 test strings; this combination makes 8265 unique pattern-string pairs. I repeat calls 10,000 times to get a better time resolution, and therefore every function's called 82,650,000 times. You can download the test code here.
Algorithm Time (s) -------------------------------------- Iterative 0.890 Iterative Optimised 0.740 Kirk J. Krauss 1.222 Alessandro Cantatore 1.291 NFA 2.276 7Zip Recursive 860.000
As an obvious result, recursive algorithms are not an option if we want speed. They are small and simple, but just a little longer iterative alternatives give a substantial amount of speed improvement (~1000 times).
NFA algorithm turned out to be slower than backtracking ones with my test set. It was expected because unlike regex, wildcards don't have optional quantifiers or alternation constructs, hence they don't suffer from backtracking as much. Most of the times, backtracking is faster than keeping all the possible matches in a list and comparing them as you iterate string.
I was able to create pattern and string instances that lead to heavy backtracking and prove that NFA performs better in such cases. But they were very long and artificial, in real world scenarios, simple iterative algorithms mostly outperforms the NFA algorithm.
Please contact me if you find a bug in one of these functions. You can also contact me if you have a suggestion, question or flame.